이전 포스팅에서 에디터에 피킹기능을 추가하기전에 해야할 작업이 있었습니다. 바로 빛 오브젝트의 위치에 빌보드를 띄우는것인데요. 빌보드는 한마디로 카메라를 바라보는 평면기하구조에 텍스쳐를 입힌것이라고 생각하면되겠습니다. 실제로 파티클 효과에 빌보드가 많이사용됩니다.
그냥 흰색 원구를 빛위치에 띄우는것보다 빌보드를 통해 빛오브젝트를 표현하는게 좀 더 예쁠것같아요
빌보드 튜토리얼 링크는 아래있습니다.
http://www.opengl-tutorial.org/intermediate-tutorials/billboards-particles/billboards/
Billboards
Billboards are 2D elements incrusted in a 3D world. Not a 2D menu on top of everything else; not a 3D plane around which you can turn; but something in-between, like health bars in many games. What’s different with billboards is that they are positionned
www.opengl-tutorial.org
원리는 정말 간단한데요. 일단 사각형을 구성할 정점을 정의해야합니다. 빌보드가 될 중점위치로부터 좌상단,좌하단,우상단,우하단 4개의 정점이 필요합니다.
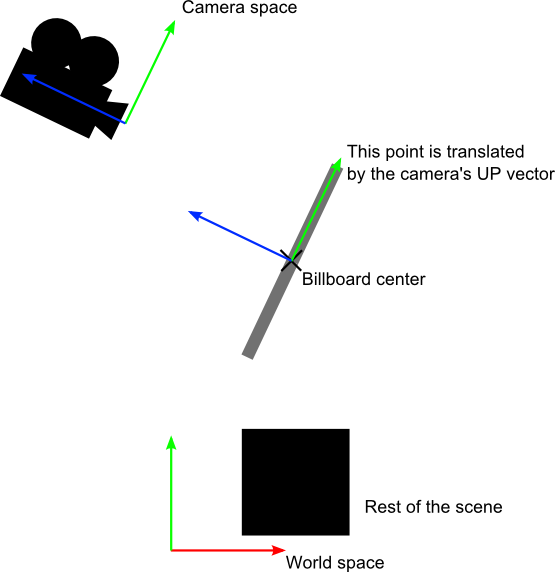
4개의 정점을 구하고 그리고 그렇게 구성된 평면이 카메라를 바라보게하려면 어떻게 해야할까요? 위 이미지에서 힌트를 얻을 수 있습니다. 선형대수학을 배우셨다면 우리가 매일 다루는 행렬속에 3차원을이루는 기저축이 존재한다는것을 알 고 계실겁니다 보통 Right,Up,Forward 벡터로 알고있으며 이 3개의 벡터로 3차원의 모든 좌표를 나타낼 수 있구요. 그리고 이 기저축의 값에따라 회전이나 스케일을 수행하게됩니다. (4행의 위치벡터는 선형이아닙니다)
그렇다면 위 이미지에서 보이는것처럼 빌보드의 중심좌표가있다면 나머지 4개의 정점은 어떤 기저축을 따르면 카메라를 항상 바라볼까요? 바로 카메라의 Up,Right 벡터와 동일선상에 존재하게되면 항상 바라보는 평면이 만들어질것입니다.
이런과정없이 그냥 길이가 각각 1인 4개의 정점에 현재 카메라와 중심좌표사이의 각도를 구해서 평면을 회전시키는방법도 나쁘지않습니다만 행렬연산보다 4개의 정점을 만들어서 사용하는게 더 연산량이 작을거라고 생각해요.
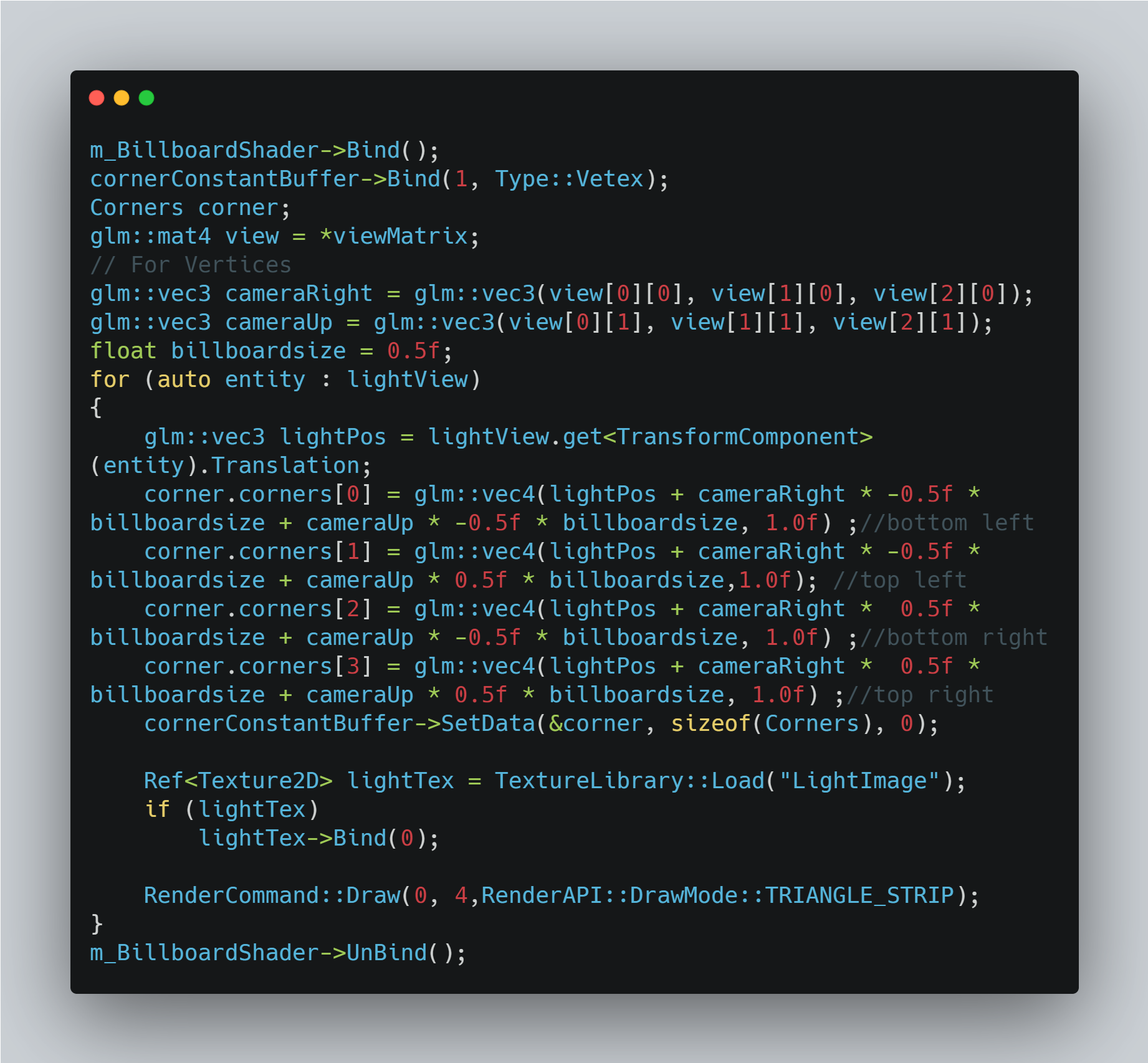
빌보드 렌더링하는 코드입니다. 저는 여기서 정점버퍼와 인덱스버퍼를 구성하지 않고사용하는데요 사실 카메라의 위치에따라 계속해서 정점의 위치가 바뀌다보니 다이나믹 정점버퍼로 만들어서 프레임마다 계속 갱신해줘야합니다. 물론 큰 연산을 아니겠지만 그렇게 정점버퍼를 만들기는 귀찮더라구요 그래서 좀더 좋은방법을 생각했습니다.
일단 DirectX 에서는 Draw 함수 호출시 바인딩된 정점버퍼가 없더라도 정점쉐이더를 호출하게됩니다. 우리는 여기서 0의위치에서 4개의 정점개수를 Draw하니 정점쉐이더는 4번 호출되게됩니다.
그리고 준비한 빌보드중심 상하좌우 정점의 위치는 ConstantBuffer, uniformBuffer 로전달합니다. 여기서 주의점은 카메라의 Right Vector과 Up Vector를 사용하여 중점위치로부터 4개의 정점을 만든다는것입니다. 자 그렇다면 4번의 Draw호출과함께 준비한 정점을 버퍼에 올린것까지 좋습니다. 그렇담 텍스쳐좌표는 안정해져있는데 어떻게 정해줘야할까요?
호출 순서에따라 UV 값을 전달해주는 방법이 있을까요? 아래는 빌보드 정점 쉐이더 코드입니다.
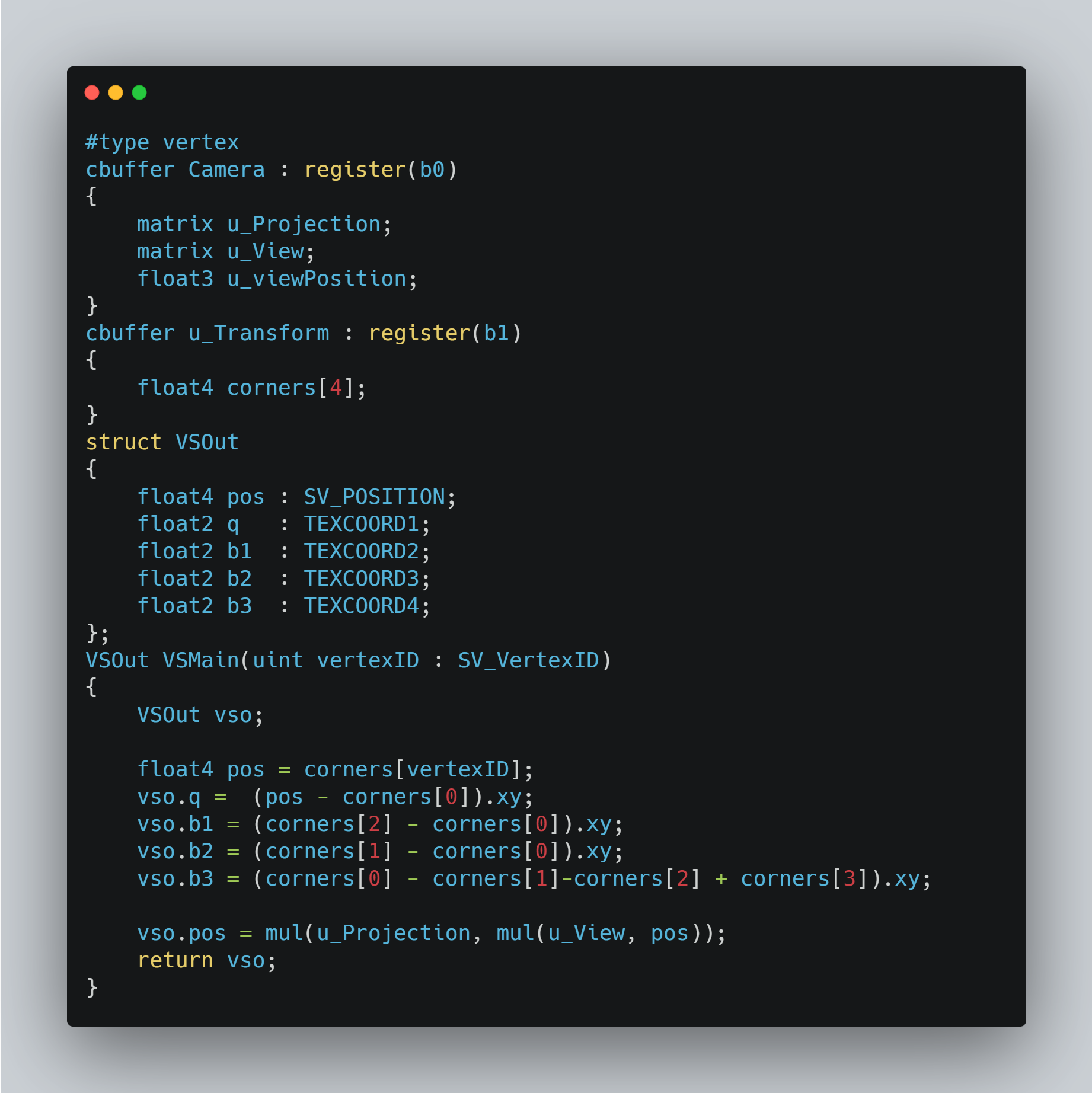
일단 기본적으로 클립공간으로 정점을 변환해야하는것은 똑같습니다. 이렇게 변환한 정점은 월드상에 존재하며 각 코너 정점값을 이용하여 2차원벡터를 만들어서 픽쉘쉐이더에 전달합니다 여기서 중요한점은 SV_VertexID 키워드입니다. 정점쉐이더가 호출되면 정점에 ID값이 붙게되는데요 우리는 4개의 정점을 전달한다고 Draw함수를 호출했으니 정점쉐이더에는 4번의 정점쉐이더 호출과함께 4개의 ID 값이 오게됩니다. 이렇게 들어온 ID값을 이용하여 2차원벡터들을 만들고 픽쉘쉐이더에 전달합니다. 근데 어떤 작업을 하는것일까요?
https://www.reedbeta.com/blog/quadrilateral-interpolation-part-2/
Quadrilateral Interpolation, Part 2 – Nathan Reed’s coding blog
www.reedbeta.com
이 방법은 위 링크에서 확인 할 수 있습니다.
기사를 요약하자면 사각형에 텍스쳐를 매핑했을때 발생하는 왜곡,줄 현상에대해 설명하는 글이며 임의의 아핀변환을 거친 사각형에 텍스쳐이미지를 입힐수있게하는것이 선형보간입니다.

위 이미지에서 보듯이 스케일값이 변하거나 회전을하여도 텍스쳐이미지가 잘 입혀지게되는데요.

하지만 하나의 정점을 움직여서 더이상 평행하지않게 만들고 이런 구조의 메쉬에 텍스쳐를 입히게되면 경계선이 보이는듯한 효과가 나오게됩니다. 이러한 현상은 삼각형들이 UV 공간에서는 여전히 하나이기 때문인데요 UV공간에서는 여전히 각 정점이 0.0~1.1 의 부분을 차지하고있지만 모델공간에서는 더이상 동일하지않습니다. 이 두 삼각형에 적용되는 아핀변환들은 더이상 같게 적용되지 않아요 .
일반적으로 불규칙한 모양의 기하구조를 만들때 UV값을 위 메쉬처럼 각 점이 사각형마냥 가지도록 하지않을겁니다. 레벨디자이너가 불규칙한 모양의 벽을 만들때에는 해당 불규칙한 벽에 알맞은 UV값을 지정해줄것이고요 그렇게하여 삼각형이 동일한 아핀변환을 받으면 그것은 불규칙한벽에 텍스쳐를 씌울때 왜곡이 일어나지않는것이니 모든 텍스쳐가 보이진 않을거에요 말그대로 아래로 처진 정점은 다렉기준 1,0 이아니라 (1,0.4) 정도로 지정해서 만들겁니다.
하지만 우리가 임의의 4각형을 왜곡없이 텍스쳐를 입히고 싶다면 어떻게 해야할까요? 기사의 첫번째 글에서는 Perspective Interplation 이란 방법을 통해 해결했지만 그것도 완벽한 해결법은 아니었습니다.
제가 저렇게 들어온 4개의 정점에대한 텍스쳐좌표를 얻어낼때 사용한 방법은 아래와 같습니다.

이중선형보간을통해 텍스쳐좌표를 얻는것입니다. 위 이미지는 텍스쳐샘플링때 이중선형보간에대한 이미지인데요 저기 가운데에있는 녹색점의 색깔을 결정하는방법은 주변 4개의 텍셀값과 현재 찍힌 위치사이의 이중선형보간을통해 얻어지는 결과입니다. 말그대로 첫번째로 t0 텍셀과 t1 텍셀 사이의 보간을 현재 u 값을 기준으로 진행하고 동시에 위에서 t2,t3에대한 선형보간결과 이 두개의 결과를 다시 v를 기준으로 보간하는 것입니다.
이때 보간식을 표현하면
p(u,v)=lerp(lerp(p0,p1,u),lerp(p2,p3,u),v)

이제 수학식이 나오는데 구현만 보고싶으신분은 넘어가셔도 무방합니다. 위에서 보았듯이 이중선형보간은 쿼드안의 UV좌표에 관한 점의 위치를 나타냅니다. P0~P3를 쿼드의 정점이라고 생각하고 (어떤 공간에서든지 쿼드안의 정점) 그러면 위치들은 주어진 UV에 부합합니다.
0=(p0−p)+(p1−p0)u+(p2−p0)v+(p0−p1−p2+p3)uv

여기서 갑자기 P가 나왔다고 헷갈리지마시고 P는 왼쪽항에있던 p(u,v)입니다. P점의 uv값이지만 UV값을 구하기위해 포지션 P로 오른쪽항으로 넘겨줍니다. 괄호안의 4개의 벡터는 쉽게 기하학적으로 해석될 수 있습니다. UV 공간의 오리진에 연관된 픽셀위치를 가지고있고 2개의 UV기저벡터를 가지고있습니다. 그리고 하나더 P0-P1-P2+P3 이 벡터는 쿼드가 평행사변형으로부터 얼마나 벗어났는지 알려주는 벡터입니다. 즉 위 이미지의 P3를 의미하는데, 평행4변형을 이루기위한 원래 위치인 UV 기저벡터를 사용하여 늘어난 완벽한 평행4변형과 P3 사이의 차이입니다.
(저도 정확하게 왜 P3가 저렇게 벗어나는정도를 표현해야하는지 이해가 안가더라구요 P2,P1도 저렇게 벗어난 정도를 표현할수 있어야하지 않나 생각해봅니다)
q = p - p0
b1 = p1 - p0
b2 = p2 - p0
b3 = p0 - p1 - p2 + p3
편리성을 위해 각각의 벡터에 이름을 정해주고우리가 풀려는 등식은 아래와 같아집니다.
0=−q+b1u+b2v+b3uv(∗)
U를 구하기위해 v관점에서 문제를 해결해봅시다.
q - b2v = (b1+ b3v)u
u = (q-b2v)/(b1 + b3v)
여기서 짚고넘어가야할 문제가 있습니다. U를 구하기위해 식을정리하던중 벡터로 벡터를 나누는 상황이 나왔는데요. 알다시피 벡터로 벡터를 나눌수는 없습니다. 다만 기사에서는 정확히 V를 계산했다면 분모와 분자는 서로 반드시 평행해야합니다. 그래서 u 값을 얻기위해 서로 나누기가 가능하다는 것입니다 (그리고 u 값은 스칼라 값이 나오겠지요) 이것을 구현하기위해 벡터 좌표중 하나의 요소를 고를것입니다 (즉 벡터들이 서로 평행하다는 가정하에 나누기 연산을위해 벡터의 요소중 하나를 사용하여 스칼라계산을 한다는뜻)
위 식에서 이제 V 값을 구하기위해 등식(*) 에서 U 를 제거할 수 있습니다. 여기서 쇄기곱이라는 개념이나오는데요. 쇄기곱이란 벡터의 외적과 유사하지만 벡터의 외적이 또다른 벡터를 산출하는것과다르게 쇄기곱은 방향성을 가진 평면을 의미하는 이중벡터(bivector)를 산출하게됩니다. 정확히는 미분기하학을 들으시면 알 수 있지만 저도 잘모릅니다.. 검색해보면서 쇄기곱은 같은 자기자신과 쇄기곱을 수행하게되면 0이나오는 성질을 이용하여 u값을 제거할것입니다.고로 아래 등식에서 u앞에있는 (b1+b3v)에대한 쇄기곱을 양쪽항에 진행하게되면
0=(−q+b1u+b2v+b3uv)∧(b1+b3v)
=(b1∧q)+(b3∧q−b1∧b2)v+(b2∧b3)v2
U값은 사라지게되고 위 식 처럼 정리할 수 있습니다. 즉 처음에 (b1+b3v)u ^ (b1+b3v) 는 0 * U 가되어버려 U값이 없어지게되고 건너편 항인 (q-b2v) ^(b1+b3v)=0 을 전개했을때 위 식처럼 나오는것입니다.
이제 이식을가지고 2차방정식의 근의법칙을 이용하여 v 값을 구할것입니다. 그렇다면

ABC 각항을 치환하게되면 위처럼 나오고 이것을통해 v값을 구할 수 있습니다.
u = (q-b2v)/(b1 + b3v)
V값을 구했다면 위식을 통해 U값을 구할 수 있구요!
실제 하나씩 대입하여 계산해보면 UV값이 구해지는걸 알 수 있습니다. 위 이미지대로 uv값을 구하게되면 p0 에는 (0,0) p1 에는 (1,0) p2 에는 (0,1) p3가 본래 있어야할 평행사변형을 이루기위한 위치에있다면 (1,1)이 나오게되고 그래서 쉐이더에 데이터를 전달하실때 p0,p1,p2,p3 에대한 정보를 각 텍스쳐 좌표계에 따라 그리고 정점 감기 방향에 따라 적절하게 전달해야합니다.
저는 ClockWise 시계방향으로 정점을 감으므로 p2의 값은 순서대로 정점을 전달해주므로 Corners 값의 [1] 에해당합니다. 그리고 p1의 값은 Corners값의[2]에 해당하구요
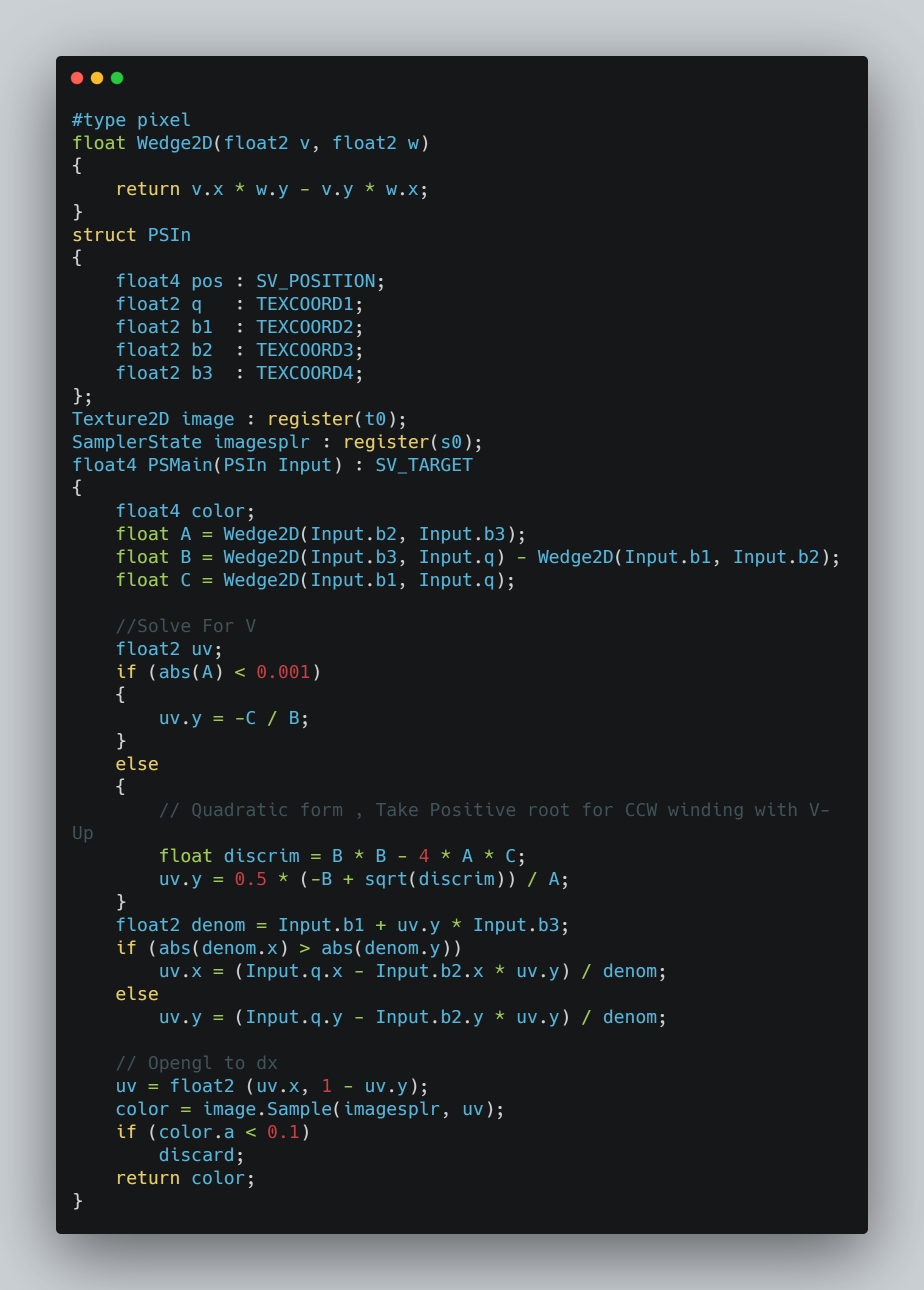
픽쉘쉐이더 입니다. Wedge2D 함수는 쇄기곱 연산을 해주는 함수입니다. 근의방정식을 이용하여 V값을 구하고 여기서 +부호를 선택하게되면 CCW라는데 부호를 바꾸어도 결과는 달라지지않아서 정확하게 어떤의미인지는 모르겠습니다. 실제로 계산해보면 -1 값이 V값으로 나오는경우가있어서
정점쉐이더에서 TopLeft 정점위치를 corners[1]에 넣어줬으므로 b2를 구성할때 corners[1] - corners[0] 로 구하는것에 유의하시고 계산하시면 직접 텍스쳐좌표를 정의하지 않고 계산식을통해 4개정점에대한 텍스쳐좌표를 이중보간을통해 얻을 수 있습니다.

이제 원형구가아닌 빌보드를통해 라이트를 나타냅니다. (직접그려서 되게 이상하네요!)
'그래픽스' 카테고리의 다른 글
| 스텐실 버퍼를 사용한 외곽선효과 및 삼각형으로 풀스크린 그리기 (0) | 2021.08.16 |
|---|---|
| ID값을 기록한 텍스쳐를 사용하여 3D오브젝트 피킹하기 (0) | 2021.08.13 |
| Assimp 를 이용하여 모델불러오기 (0) | 2021.08.10 |
| 다중광원과 그림자 구현하기 (Multiple Light and Shadow) - 스폿라이트 (0) | 2021.08.06 |
| 다중광원과 그림자 구현하기 (Multiple Light and Shadow) - 포인트라이트 (0) | 2021.08.05 |



